Other articles

  1. How Many Boxes are on the Trailer?

    I recently came across an interesting puzzle:

    Without shading or a 3D-view, we can not give a definitive answer. Taking a look at the side view, we can give an upper bound. If we expect, from the side view, every visible cube to have two invisible boxes behind it, we get to 51 cubes. But what is the lower bound?

    I thought, it would be a good idea and exercise, to solve this problem using a constraint solver. First I needed to decide on a model. As there exists a grid of \(7*3*3\) fields where each contains either a box or it does not. That sounds suspiciously like something Boolean. So let's model it as a Boolean satisfiability problem (SAT).

    Since I haven't before, I wanted to try out PySAT and take it for a spin: The SAT solvers work with Boolean variables without names, just numbers. Additionally, our interface will create additional variables when we create more complex formulas due to Tseytin transformation. Tseytin transformation essentially creates a variable representing a subformula and the constraints for equivalence between the valuation of the newly created variable and the subformula. If you now want to create a new formula that contains the original formula as a subformula, you can refer to the single newly created variable, representing the whole subformula.

    Because, as I said, the interface with the solver will be numbers-based, we need to decide on some representation or indexing between the solver's variables and our domain. We'll use a namedtuple for a Position P on the trailer, where x is along the depth of the trailer when viewed from the back, y is along the width of the trailer when viewed from the back, and z is along the height of the trailer, with the origin being at the bottom front left. We also need an empty list of constraints that we add to along the way:

    from pysat.formula import *
from collections import namedtuple

P = namedtuple('P', ['x', 'y', 'z'])

boxes = {}

depth = 7
width = 3
height = 3

for x in range(depth):
  for y in range(width):
    for z in range(height):
      boxes[(x,y,z)] = Atom(P(x,y,z))

constraints = []

    Instead of a namedtuple i initially wanted to use anonymous 3-tuples, but a bug in the library prevented me from doing that.

    First we want to create the constraints for the side view. If we can see a box from that side, we know that at least one space in that group of 3 is filled by a box. We can simply use a disjunction over those three variables. If the space is empty, we know that there are no boxes. We can negate the disjunction. We "draw" the shape to make sure we got it right:

    # side view
X = True
O = False
side_view = [
  [X,X,X,X,O,O,O],
  [X,X,X,X,X,X,O],
  [X,X,X,X,X,X,X],
]
for x in range(depth):
  for z in range(height):
    if side_view[-z-1][x]:
      constraints.append(Or(*[boxes[(x,y,z)] for y in range(width)]))
    else:
      constraints.append(Neg(Or(*[boxes[(x,y,z)] for y in range(width)])))

    For the top view and back view we do not need to draw the shape that we are seeing, because every row/column/stack has a box in it and we do not need to consider the other case.

    # back view
for y in range(width):
  for z in range(height):
    constraints.append(Or(*[boxes[(x,y,z)] for x in range(depth)]))

# top view
for y in range(width):
  for x in range(depth):
    constraints.append(Or(*[boxes[(x,y,z)] for z in range(height)]))

    This looks like we are finished, but we have not yet considered gravity. If a box is anywhere not on the bottom level, it has to have another box under it. That is an implication:

    # gravity
for x in range(depth):
  for y in range(width):
    for z in range(height-1):
      constraints.append(Implies(boxes[(x,y,z+1)], boxes[(x,y,z)]))

    When I tried this out initially, there was a bug in the pySAT library where you could not use implications that are not on the top-level. This has been fixed quite fast.

    Now we want to know the minimum number of needed boxes. We will get one solution, check how many boxes we needed, and add a constraint that we want one box less. We will do this until our formula is no longer satisfiable.

    f = And(*constraints)

from pysat.solvers import Solver
with Solver(bootstrap_with=f) as solver:
  while solver.solve():
    model = solver.get_model()
    atoms = Formula.formulas((b for b in model if b > 0), atoms_only=True)
    boxes_needed = len(atoms)
    print("Solution with", boxes_needed, "boxes found")
    print(atoms)
    print("="*80)

    from pysat.card import CardEnc
    solver.append_formula(CardEnc.atmost(f.literals(boxes.values()), boxes_needed-1, vpool=Formula.export_vpool()))

    It is important, when counting boxes, that we only extract the formulas/atoms that we created and not the ones created internally due to Tseyitin transformation. We count them and add a cardinality constraint, where we say, that we want at most one box less than we currently have used. An after only three iterations we get the following result:

    Solution with 33 boxes found
[Atom(P(x=0, y=0, z=0)), Atom(P(x=0, y=1, z=0)), Atom(P(x=0, y=2, z=0)), Atom(P(x=0, y=1, z=1)), Atom(P(x=0, y=2, z=1)), Atom(P(x=0, y=1, z=2)), Atom(P(x=0, y=2, z=2)), Atom(P(x=1, y=0, z=0)), Atom(P(x=1, y=1, z=0)), Atom(P(x=1, y=2, z=0)), Atom(P(x=1, y=0, z=1)), Atom(P(x=1, y=0, z=2)), Atom(P(x=2, y=0, z=0)), Atom(P(x=2, y=1, z=0)), Atom(P(x=2, y=2, z=0)), Atom(P(x=2, y=0, z=1)), Atom(P(x=2, y=0, z=2)), Atom(P(x=3, y=0, z=0)), Atom(P(x=3, y=1, z=0)), Atom(P(x=3, y=2, z=0)), Atom(P(x=3, y=0, z=1)), Atom(P(x=3, y=0, z=2)), Atom(P(x=4, y=0, z=0)), Atom(P(x=4, y=1, z=0)), Atom(P(x=4, y=2, z=0)), Atom(P(x=4, y=0, z=1)), Atom(P(x=5, y=0, z=0)), Atom(P(x=5, y=1, z=0)), Atom(P(x=5, y=2, z=0)), Atom(P(x=5, y=0, z=1)), Atom(P(x=6, y=0, z=0)), Atom(P(x=6, y=1, z=0)), Atom(P(x=6, y=2, z=0))]
================================================================================
Solution with 32 boxes found
[Atom(P(x=0, y=0, z=0)), Atom(P(x=0, y=1, z=0)), Atom(P(x=0, y=2, z=0)), Atom(P(x=0, y=0, z=1)), Atom(P(x=0, y=0, z=2)), Atom(P(x=1, y=0, z=0)), Atom(P(x=1, y=1, z=0)), Atom(P(x=1, y=2, z=0)), Atom(P(x=1, y=1, z=1)), Atom(P(x=1, y=1, z=2)), Atom(P(x=2, y=0, z=0)), Atom(P(x=2, y=1, z=0)), Atom(P(x=2, y=2, z=0)), Atom(P(x=2, y=0, z=1)), Atom(P(x=2, y=2, z=1)), Atom(P(x=2, y=2, z=2)), Atom(P(x=3, y=0, z=0)), Atom(P(x=3, y=1, z=0)), Atom(P(x=3, y=2, z=0)), Atom(P(x=3, y=0, z=1)), Atom(P(x=3, y=0, z=2)), Atom(P(x=4, y=0, z=0)), Atom(P(x=4, y=1, z=0)), Atom(P(x=4, y=2, z=0)), Atom(P(x=4, y=2, z=1)), Atom(P(x=5, y=0, z=0)), Atom(P(x=5, y=1, z=0)), Atom(P(x=5, y=2, z=0)), Atom(P(x=5, y=2, z=1)), Atom(P(x=6, y=0, z=0)), Atom(P(x=6, y=1, z=0)), Atom(P(x=6, y=2, z=0))]
================================================================================
Solution with 31 boxes found
[Atom(P(x=0, y=0, z=0)), Atom(P(x=0, y=1, z=0)), Atom(P(x=0, y=2, z=0)), Atom(P(x=0, y=0, z=1)), Atom(P(x=0, y=0, z=2)), Atom(P(x=1, y=0, z=0)), Atom(P(x=1, y=1, z=0)), Atom(P(x=1, y=2, z=0)), Atom(P(x=1, y=2, z=1)), Atom(P(x=1, y=2, z=2)), Atom(P(x=2, y=0, z=0)), Atom(P(x=2, y=1, z=0)), Atom(P(x=2, y=2, z=0)), Atom(P(x=2, y=0, z=1)), Atom(P(x=2, y=0, z=2)), Atom(P(x=3, y=0, z=0)), Atom(P(x=3, y=1, z=0)), Atom(P(x=3, y=2, z=0)), Atom(P(x=3, y=1, z=1)), Atom(P(x=3, y=1, z=2)), Atom(P(x=4, y=0, z=0)), Atom(P(x=4, y=1, z=0)), Atom(P(x=4, y=2, z=0)), Atom(P(x=4, y=2, z=1)), Atom(P(x=5, y=0, z=0)), Atom(P(x=5, y=1, z=0)), Atom(P(x=5, y=2, z=0)), Atom(P(x=5, y=2, z=1)), Atom(P(x=6, y=0, z=0)), Atom(P(x=6, y=1, z=0)), Atom(P(x=6, y=2, z=0))]
================================================================================

    Now we know that the lower bound on boxes is 31. But what does such a solution look like? Let us plot them using matplotlib, putting them all in a three-dimensional array

    import matplotlib.pyplot as plt
import numpy as np

# Prepare some coordinates
x, y, z = np.indices((depth, depth, depth))

cubes = [((atom.object.x == x) & (atom.object.y == y) & (atom.object.z == z) )  for atom in atoms]

# Combine the objects into a single boolean array
voxelarray = cubes[0]
for cube in cubes[1:]:
  voxelarray |= cube

# Plot
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
ax.voxels(voxelarray, edgecolor='k')

ax.set(xticklabels=[], yticklabels=[], zticklabels=[])

plt.show()

    And here is our trailer in glorius 3D:

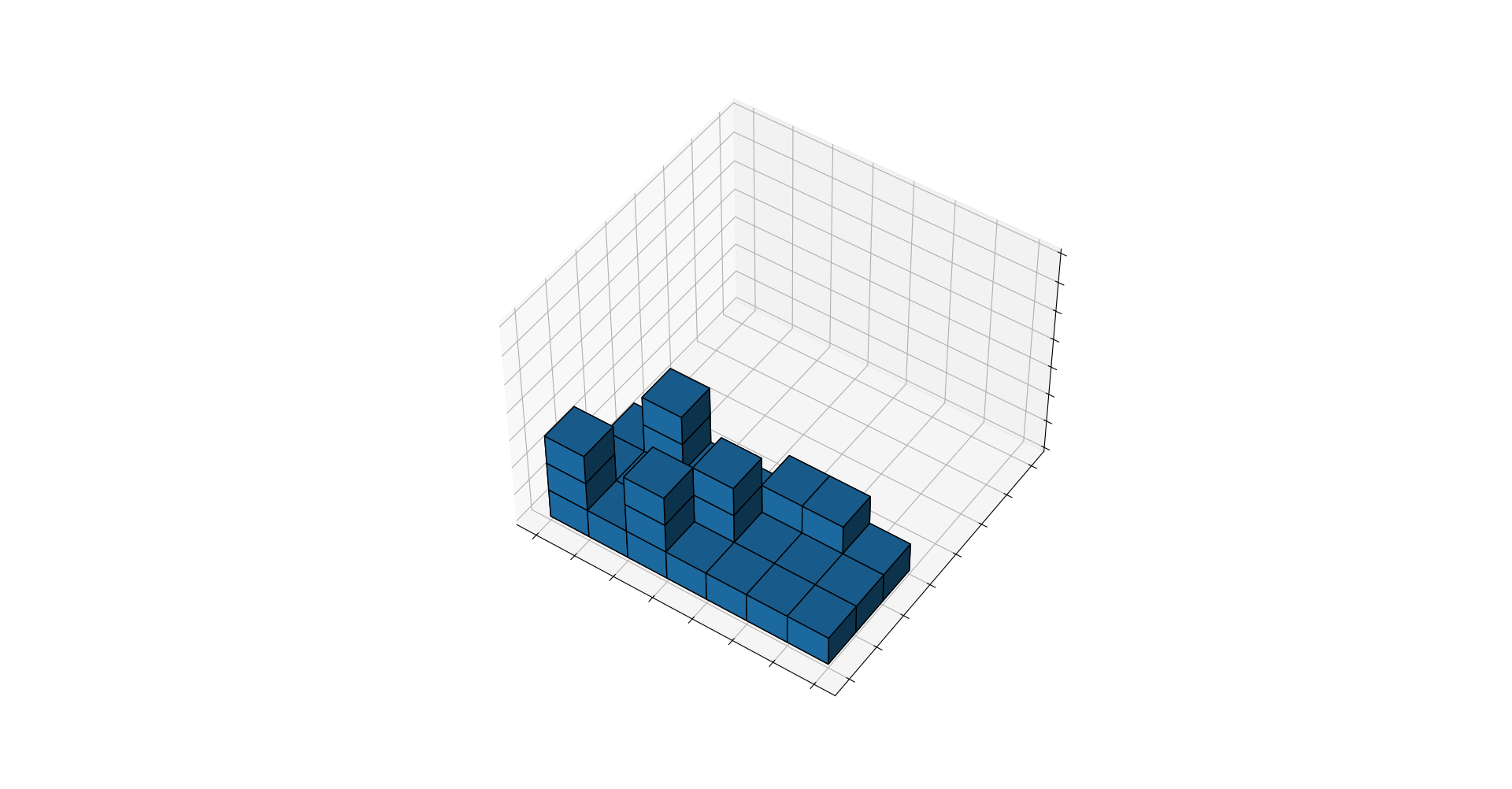
    Obviously the solution is not unique, as some stacks can be swapped and the whole configuration can be mirrored.

    And just out of curiosity, if there were no gravity...

    Solution with 26 boxes found
[Atom(P(x=0, y=0, z=0)), Atom(P(x=0, y=1, z=1)), Atom(P(x=0, y=2, z=1)), Atom(P(x=0, y=1, z=2)), Atom(P(x=0, y=2, z=2)), Atom(P(x=1, y=1, z=0)), Atom(P(x=1, y=2, z=0)), Atom(P(x=1, y=0, z=1)), Atom(P(x=1, y=0, z=2)), Atom(P(x=2, y=1, z=0)), Atom(P(x=2, y=2, z=0)), Atom(P(x=2, y=0, z=1)), Atom(P(x=2, y=0, z=2)), Atom(P(x=3, y=1, z=0)), Atom(P(x=3, y=2, z=0)), Atom(P(x=3, y=0, z=1)), Atom(P(x=3, y=0, z=2)), Atom(P(x=4, y=1, z=0)), Atom(P(x=4, y=2, z=0)), Atom(P(x=4, y=0, z=1)), Atom(P(x=5, y=1, z=0)), Atom(P(x=5, y=2, z=0)), Atom(P(x=5, y=0, z=1)), Atom(P(x=6, y=0, z=0)), Atom(P(x=6, y=1, z=0)), Atom(P(x=6, y=2, z=0))]
================================================================================
Solution with 25 boxes found
[Atom(P(x=0, y=2, z=0)), Atom(P(x=0, y=2, z=1)), Atom(P(x=0, y=0, z=2)), Atom(P(x=0, y=1, z=2)), Atom(P(x=1, y=2, z=0)), Atom(P(x=1, y=1, z=1)), Atom(P(x=1, y=0, z=2)), Atom(P(x=1, y=2, z=2)), Atom(P(x=2, y=2, z=0)), Atom(P(x=2, y=1, z=1)), Atom(P(x=2, y=0, z=2)), Atom(P(x=2, y=2, z=2)), Atom(P(x=3, y=2, z=0)), Atom(P(x=3, y=2, z=1)), Atom(P(x=3, y=0, z=2)), Atom(P(x=3, y=1, z=2)), Atom(P(x=4, y=1, z=0)), Atom(P(x=4, y=2, z=0)), Atom(P(x=4, y=0, z=1)), Atom(P(x=5, y=1, z=0)), Atom(P(x=5, y=2, z=0)), Atom(P(x=5, y=0, z=1)), Atom(P(x=6, y=0, z=0)), Atom(P(x=6, y=1, z=0)), Atom(P(x=6, y=2, z=0))]
================================================================================
Solution with 24 boxes found
[Atom(P(x=0, y=2, z=0)), Atom(P(x=0, y=2, z=1)), Atom(P(x=0, y=0, z=2)), Atom(P(x=0, y=1, z=2)), Atom(P(x=1, y=2, z=0)), Atom(P(x=1, y=1, z=1)), Atom(P(x=1, y=0, z=2)), Atom(P(x=1, y=2, z=2)), Atom(P(x=2, y=2, z=0)), Atom(P(x=2, y=1, z=1)), Atom(P(x=2, y=0, z=2)), Atom(P(x=2, y=2, z=2)), Atom(P(x=3, y=2, z=0)), Atom(P(x=3, y=1, z=1)), Atom(P(x=3, y=0, z=2)), Atom(P(x=4, y=1, z=0)), Atom(P(x=4, y=2, z=0)), Atom(P(x=4, y=0, z=1)), Atom(P(x=5, y=1, z=0)), Atom(P(x=5, y=2, z=0)), Atom(P(x=5, y=0, z=1)), Atom(P(x=6, y=0, z=0)), Atom(P(x=6, y=1, z=0)), Atom(P(x=6, y=2, z=0))]
================================================================================
Solution with 23 boxes found
[Atom(P(x=0, y=2, z=0)), Atom(P(x=0, y=2, z=1)), Atom(P(x=0, y=0, z=2)), Atom(P(x=0, y=1, z=2)), Atom(P(x=1, y=2, z=0)), Atom(P(x=1, y=1, z=1)), Atom(P(x=1, y=0, z=2)), Atom(P(x=1, y=2, z=2)), Atom(P(x=2, y=2, z=0)), Atom(P(x=2, y=1, z=1)), Atom(P(x=2, y=0, z=2)), Atom(P(x=3, y=2, z=0)), Atom(P(x=3, y=1, z=1)), Atom(P(x=3, y=0, z=2)), Atom(P(x=4, y=1, z=0)), Atom(P(x=4, y=2, z=0)), Atom(P(x=4, y=0, z=1)), Atom(P(x=5, y=1, z=0)), Atom(P(x=5, y=2, z=0)), Atom(P(x=5, y=0, z=1)), Atom(P(x=6, y=0, z=0)), Atom(P(x=6, y=1, z=0)), Atom(P(x=6, y=2, z=0))]
================================================================================
Solution with 22 boxes found
[Atom(P(x=0, y=2, z=0)), Atom(P(x=0, y=1, z=1)), Atom(P(x=0, y=0, z=2)), Atom(P(x=1, y=1, z=0)), Atom(P(x=1, y=0, z=1)), Atom(P(x=1, y=2, z=2)), Atom(P(x=2, y=0, z=0)), Atom(P(x=2, y=2, z=0)), Atom(P(x=2, y=0, z=1)), Atom(P(x=2, y=1, z=2)), Atom(P(x=3, y=0, z=0)), Atom(P(x=3, y=2, z=1)), Atom(P(x=3, y=1, z=2)), Atom(P(x=4, y=0, z=0)), Atom(P(x=4, y=2, z=0)), Atom(P(x=4, y=1, z=1)), Atom(P(x=5, y=1, z=0)), Atom(P(x=5, y=2, z=0)), Atom(P(x=5, y=0, z=1)), Atom(P(x=6, y=0, z=0)), Atom(P(x=6, y=1, z=0)), Atom(P(x=6, y=2, z=0))]
================================================================================
Solution with 21 boxes found
[Atom(P(x=0, y=1, z=0)), Atom(P(x=0, y=0, z=1)), Atom(P(x=0, y=2, z=2)), Atom(P(x=1, y=1, z=0)), Atom(P(x=1, y=2, z=1)), Atom(P(x=1, y=0, z=2)), Atom(P(x=2, y=0, z=0)), Atom(P(x=2, y=1, z=1)), Atom(P(x=2, y=2, z=2)), Atom(P(x=3, y=2, z=0)), Atom(P(x=3, y=0, z=1)), Atom(P(x=3, y=1, z=2)), Atom(P(x=4, y=0, z=0)), Atom(P(x=4, y=1, z=0)), Atom(P(x=4, y=2, z=1)), Atom(P(x=5, y=0, z=0)), Atom(P(x=5, y=2, z=0)), Atom(P(x=5, y=1, z=1)), Atom(P(x=6, y=0, z=0)), Atom(P(x=6, y=1, z=0)), Atom(P(x=6, y=2, z=0))]
================================================================================

  2. NULLS NOT DISTINCT in SQLite Unique Indexes

    Recently I had the problem that I needed a unique index in an SQLite database, but some fields of my table had null values, which I needed to be considered equal, or NOT DISTINCT. Some database systems allow to specify the behaviour when creating indexes, but SQLite only supports the NULLS DISTINCT behaviour. In this article, we explore two ways to express the NULLS NOT DISTINCT behaviour in SQLite.

    Not considering null values, two tuples are equal iff each of their components are equal. (1, 2, 3) is equal to (1, 2, 3). There are usually two ways to view null in databases: the absence of a value, or a value that exists but is not known.

    In "absence of a value", we would consider (1, 2, null) to be equal to (1, 2, null), as we actually mean something akin to (1, 2), i.e. NULLS NOT DISTINCT. In "unknown value", we would consider (1, 2, null) to not be equal to (1, 2, null), as null represents an unknown but possibly or probably different value in either case, i.e. NULLS DISTINCT.

    In our example we will consider an index on the table t with columns c1, c2, c3, where c1 is never null, but the other two columns can be.

    Indexes on Expressions

    One possible way (which I ultimately chose) is using indexes on expressions. Per column we choose a value which the column should never normally have. As the columns are untyped in SQlite, this is quite easy. You could choose a very large (or negative) number, or a random string. Again, some value you're fairly certain, your actual data is never going to be equal to. As an example, we choose -1, as my numbers are usually all positive. If you want to prevent accidentally using this value, you may exclude it using a CHECK-constraint.

    Now instead of creating our index as

    CREATE UNIQUE INDEX ON t (c1, c2, c3);

    we create an index on coerced values:

    CREATE UNIQUE INDEX ON t (c1, COALESCE(c2, -1), COALESCE(c3, -1));

    The COALESCE function is variadic and returns its first non-null` argument. This means, our unique index does not compare the ``null values to each other (which are not equal), but our choses non-null representative (-1 in this case).

    Problem 1: We do need a value per column that is not allowed. Often times it is very easy to find such a value. You could always use something that would be a type mismatch, or something that is malformed. But sometimes it might not be that easy and you might have to choose a different value for each column. Also, the value will be stored in the index and it should not be very large.

    Problem 2: SQLite doesn't actually use this index for queries and operations other than insert. It will not make your SELECT statements faster. So you probably want to create another index, or multiple, depending on your access patterns, that are used for retrieval. Here you can just use the original index without the UNIQUE constraint:

    CREATE INDEX ON t (c1, c2, c3);

    Our uniqueness constraint is checked through the other index.

    Partial Indexes

    The second way is to use partial unique indexes for every null/not null combination. In this way we never allow null values to sneak into our index(es) and we are back to our base case.

    CREATE UNIQUE INDEX ON t (c1) WHERE c2 IS NULL and c3 IS NULL;
CREATE UNIQUE INDEX ON t (c1, c2) WHERE c2 IS NOT NULL and c3 IS NULL;
CREATE UNIQUE INDEX ON t (c1, c3) WHERE c2 IS NULL and c3 IS NOT NULL;
CREATE UNIQUE INDEX ON t (c1, c2, c3) WHERE c2 IS NOT NULL and c3 IS NOT NULL;

    These indexes will be used by your SELECT queries and we do not need a particular value per column to trick the index checker.

    The problem with this method is obvious though, as we create \(2^n\) indexes for \(n\) nullable columns.

    So what you really want depends on your use case. Using partial indexes is probably generally faster and less error-prone, and less memory-intensive. But you do need to manage multiple (exponentially many) indexes. If you're not worried about speed and your queries are already supported by the other indexes, and you only need a simple unique constraint over nullable columns, the indexed expressions might be the variant to use.

  3. OAuth in GNOME Shell Extensions

    As you might know, I am the maintainer of the GNOME Twitchlive shell extensions. The Twitchlive panel allows you to see whether your favourite Twitch streamers are online or not.

    A few months ago, Twitch started to require OAuth authentication for its endpoints and things started to go sideways. Now there are two ways to communicate with Twitch's API:

    1. Authenticate your requests with a pre-shared application secret.
    2. Obtain a client secret through user authentication and use this secret.

    The first variant is only possible for server-to-server applications, as you're not allowed to distribute the application secret to users. So the second variant it is and we need to authenticate the user.

    In the OAuth process you open a webpage (of the oauth provider) with a callback url. That webpage contains a login form and if you enter valid credentials, the webpage will redirect you to your given callback url, passing as additional information the authorization token you can use to make a valid API call.

    To receive the token you need a webserver that you can redirect to. Even though GNOME's supposed to have a generic OAuth implementation it uses for its online services but it's not generic at all and you can't hook into that. You also can't create a webserver otherwise from within the GNOME Shell. Until a few weeks ago:

    I've implemented a small mechanism by starting a python-based webserver through the extension that has just enough capabilities to receive the OAuth token and write it to a file. As far as I know, that's a world first. If you base OAuth of you extension on this work, give me a shout on twitter.

    And now to the code which I think I boiled down right to the essentials (you'll also find it on github):

    We need to open a browser with the callback within the extension:

    function trigger_oauth() {
  const url = "https://id.twitch.tv/oauth2/authorize?response_type=token&client_id=" + client_id + "&redirect_uri=http://localhost:8877&scope=";
  GLib.spawn_command_line_async("xdg-open " + url);
  GLib.spawn_sync(null, ["python3", oauth_receiver,  oauth_token_path], null, GLib.SpawnFlags.SEARCH_PATH, null);
}

    And the python3 reciver code:

    from http.server import *;
from urllib.parse import *;
import sys;
import os.path;

page = """<html>
<head><title>Twitchlive GNOME Shell extension OAuth</title></head>
<body><script>var tokens=document.location.hash.substring(1);
document.write("<a href=\\"/tokens?" + tokens + "\\"> To finish OAuth-Process click here</a>");
</script></body>
"""

class handler(BaseHTTPRequestHandler):
  def log_requests(self):
      pass

  def do_GET(self):
      print(self.path)
      if self.path == '/':
          # initial call from twitch
          self.send_response(200)
          self.send_header("Content-Type", "text/html")
          self.end_headers()

          self.wfile.write(page.encode())
      elif self.path.startswith('/tokens'):
          # our own call
          code = parse_qs(urlparse(self.path).query)['access_token'][0]
          open(sys.argv[1], 'w').write(code)

          self.send_response(200)
          self.send_header("Content-Type", "text/plain")
          self.end_headers()

          self.wfile.write(b"Thank You. You can close this page.")
          sys.exit(0)

    Note that the OAuth-Token is passed as the url fragment that doesn't show up in the actual query so you really need a browser to read that value.

    And for now ... it works.

  4. Podcast Time Machine

    Recently one of my favourite podcasts ended after seven years. I have only been listening to this podcast for two years though. There is five year backlog for me to listen to. But there are many other podcasts I want to listen to and I do like the anticipation of waiting for a new episode.

    So I built the Podcast Time Machine (github) where you can enter a podcast url and a delay and you will get a new link where every podcast episode is delayed by that many days and all episodes that would lie in the future are filtered out. So stuff happpening a week in podcast time are happpening in a week of real time.

    I am looking forward to my first episode of harmontown, when it comes out after a seven-year delay. Feel free to subscribe to your own delayed podcasts. I do not keep access logs so listen to your favorite stuff again (and again).

Page 1 / 4 »

links

social

Theme based on notmyidea