I've started writing solvers for games of Simon Tatham's Portable Puzzle Collection. Those Problems can usually be reduced to some NP-complete problem. This is quite a fun exercise.

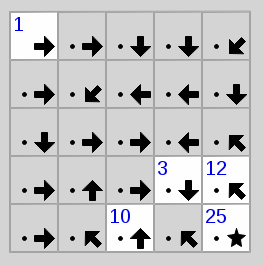
Unsolved Signpost Puzzle

We will be continuing with the puzzle "Signpost", which is a variant of Hamiltonian paths in a directed graph where, for some fields or nodes, the position within the path is given.

The goal of the puzzle is to connect the Node "1" to some node, which is then node "2" in the direction the arrow points to. All numbers need to be connected to their successor until all nodes have a single unique number from "1" to (in this example) "25".

We will be solving this problem in two different ways, both with the help of the programming language Python. But first of all we'll need to convert a puzzle into a machine readable format. Luckily, Signpost has an easy and accessible format. The problem instance from the image is the instance 5x5:1cceefcfggeeccghcac3e12hch10ah25a. It starts off with the size of the problem and then a list of letters that show the directions of the arrow where a is north or 12 o'clock and all other letters go clockwise with h being north-west. A letter can be prefixed by a number which is the hint for that node. That node's number is fixed. The cells or nodes are defined line by line from the top left to the bottom right.

Problems don't need to start with 1 or end with the last number. The start and the end of the path can be anywhere but puzzles generated with the ends at opposite corner look nicer.

First we define what our data looks like. We implement a simple form of directed graph that we define as a set of nodes and their successors. From that we derive following definition:

class Node(object):
    hint = None
    following = frozenset()

    def __init__(self, direction):
        self.direction = direction

We don't want to use any of that code in a library or something something so we don't do anything fancy here and we use the simplest class definition that comes to mind.

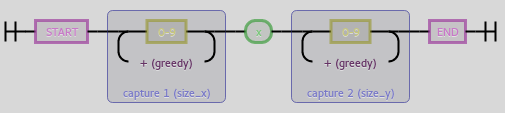
^(?P<size_x>\d+)x(?P<size_y>\d+)$

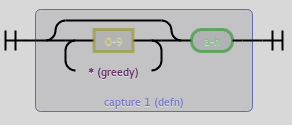
(?P<defn>\d*[a-h])

Now we go on to parsing the problem. The parsing function should get the problem as a string and return a 3-tuple containing width and height of the problem as well as a mapping of positions within the grid to ``Node`` instances.

Onto actually parsing. We can split at the colon and then regular expressions to the rescue. The size definition has the form ^(?P<size_x>\d+)x(?P<size_y>\d+)$ while a single node definition has the form (?P<defn>\d*[a-h]). As we can see, the digits are optional but we need to greedily accept them. All non-overlapping occurences in order will be our cell definitions.

In code we, again, do nothing too too fancy:

def parse(puzzle_str):
    directions = {
        'a': (0,-1), 'b': (1,-1), 'c': (1,0), 'd': (1,1),
        'e': (0,1),  'f': (-1,1), 'g': (-1,0),'h': (-1,-1)
    }

    size, _, definition = puzzle_str.partition(':')
    r_size = re.compile(r"^(?P<size_x>\d+)x(?P<size_y>\d+)$")
    r_defn = re.compile(r"(?P<defn>\d*[a-h])")
    size_t = tuple(map(int, r_size.match(size).groups()))
    w, h = size_t
    nodes = {}
    for n, m in enumerate(r_defn.finditer(definition)):
        pos = (n % w, n // w)
        nodes[pos] = Node(directions[m.group(0)[-1:]])
        hint = m.group(0)[:-1]
        if hint:
            nodes[pos].hint = int(hint)
    return w, h, nodes

And we also need to fill in the successor Nodes. This is no problem at all.

w, h, nodes = parse(sys.argv[1])
from itertools import product
for x, y in product(range(w), range(h)):
    this_node = nodes[(x,y)]
    dx, dy = this_node.direction
    x, y = x + dx, y + dy
    while x >= 0 and x < w and y >= 0 and y < h:
        this_node.following = this_node.following | frozenset([nodes[x,y]])
        x, y = x + dx, y + dy

And now on to actually solving this thing. The idea is, that we slowly build a list of Nodes that is our solution. The first element is the Node with the hint "1" and we iterate through all nodes that follow that Node and do not have a hint that is other than "2", and so on. And of course, the Node that we add to the solution is not allowed to have already been part of the solution and if there is a node with that hint, it should be this exact one. If we find such a conflict in our solution, we reject that solution and return to an earlier partial solution.

Instead of using recursion, we build a queue of partial solutions until we get a complete solution. This is functionally identical to restarting a solver function with partial solutions of increasing size. In that case, the call stack manages the backtracking. But we'll do it with a queue this time. We build the queue so that every element in the list is either

1. a partial solution (beginning from 1) without conflicts
2. a partial solution (beginning from 1) where the last element is in some conflict
3. a complete solution

For case 1, we remove the partial solution that has the length n and add all partial solutions of length n+1 by iterating through all successor Nodes that have not yet been part of the partial solution. For case 2, we reject that partial solution. For case 3, we immediately return that solution and are finished.

def solve_dhc(nodes):
    # get the Node that has hint 1
    first = next(iter(n for n in nodes.values() if n.hint == 1))
    # get the set of all hints, so it is easier to check for conflicts
    hints = frozenset(n.hint for n in nodes.values() if n.hint is not None)
    from collections import deque
    q = deque([[first]]) # initializing queue
    while q:
        curr = q.pop()
        idx = len(curr)
        if (idx in hints or curr[-1].hint is not None) and curr[-1].hint != idx:
            continue # case 2
        if idx == len(nodes):
            return curr # case 3
        for _next in curr[-1].following: # case 1
            if _next not in curr:
                q.append(curr + [_next])

This algorithm terminates because we always remove one element from the queue of some length n and possibly add a large but finite amount of elements of length n+1 and the algorithm terminates when we have an element in the queue of some possibly large but finite length.

Sidenote: if you use popleft instead of pop you get a breadth-first search instead the depth-first search, that is implemented here. Add to the right and pop from the right for depth-first and add to the right and pop from the left for breadth-first. Since every proper solution has the exact same length/depth (that we know and never go further anyways), searching depth-first is strictly better than breadth-first.

And given a solution, we still have to print it. That's the easy part.

dhc = solve_dhc(nodes)

fill = len(str(w*h))
for l in range(h):
    for c in range(w):
        node = nodes[(c,l)]
        print(str(dhc.index(node) + 1).rjust(fill), end=" ")
    print("")

Solved Puzzle

And there's the solution for our puzzle.

$ python3 signpost_dhc.py 5x5:1cceefcfggeeccghcac3e12hch10ah25a
 1 20  9  2 21
23 14 13 22 24
15  5  7  6  8
18 19 11  3 12
16 17 10  4 25

This post is part of the series "Tatham's Puzzles":

• 31.01.2016 – Solving Tatham's Puzzles - Pattern
• 21.03.2016 – Solving Tatham's Puzzles - Signpost (backtracking)

Previous: My computer science course of Jan 2016 , Next: Installing Rocket Chat with own MongoDB instance on a Raspberry Pi B