I recently bought and installed a Cluster Hat.
Looks interesting
I don't know what I will do with it. All my plans I had before hinged on Haskell supporting ARMv6, which it doesn't. Let's see what happens in the future. I am currently looking into installing Docker on it and maybe host some service through my VPS from home.
I wanted to write a bit about notation as I have seen students and programmers stumble quite a bit about this. What is "this"? When to write parentheses and commas in tuples and what does it mean.
Consider the set \(S = \{a, b\}\). Now lets take the cross product of itself. \(S \times S = \{(a,a), (a,b), (b,a), (b,b)\} = S^2\). By the same logic \(S^3 = \{(a, a,a), (a, a,b), (a, b,a), (a,b,b), (b,a,a), (b,a,b), (b,b,a), (b,b,b)\}\). This is somewhat strange since \(S^3 = S^2 \times S = S \times S^2\) meaning that these two should also be the same as \(S^3\):
\(\{(a, (a,a)), (a, (a,b)), (a, (b,a)), (a,(b,b)), (b,(a,a)), (b,(a,b)), (b,(b,a)), (b,(b,b))\} = \\ \{((a, a),a), ((a, a),b), ((a, b),a), ((a,b),b), ((b,a),a), ((b,a),b), ((b,b),a), ((b,b),b)\}\)
Let's step back a bit and look at the identity, meaning \(S^1\). We know that the power one is the identity but following the same logic as before we have the following: \(S = \{a, b\} = S^1 = \{(a), (b)\}\). The parantheses do not matter and we are supposed to think of them as just as sequence of values. Let's take a look at the empty sequence: \(S^0 = \{()\}\). Note that this is not the empty set but it is the neutral element for the cartesian product: \(\{()\} \times \{a, b\} = \{((), a), ((), b)\} = \{a, b\}\).
What is going on here? The cartesian product is, as is the normal product, an extension of some kind of addition. In our case addition is concatenation of sequences and every value is a sequence of one element (singleton sequence). This is different to the singleton set which is distinct from the value it contains. \(\{a, b\} \times \{c, d\} = \begin{Bmatrix}a \circ c \ & a \circ d\\b \circ c & b \circ d\end{Bmatrix}\) looks very much like the cross product for vectors and of course, the empty sequence is the neutral element (or identity) of that operation.
So actually we are supposed to take nested tuples as sequences of values that - in our mind - should be flattened. This also means, there is no one-tuple (it is the same as the value) and there ist just one zero-tuple.
By the way: this notation fits nicely as it just maps the cardinality of the sets. So if you just take \(S=2\) you see that all the formulas just magically work out.
Why do we even use this tuple notation? This has to do with something we call coding.
I will define code the following way: A set is a code if no two different sequences of elements of that look the same when written down consecutively (this is a layman's definition that shall suffice here). Take the set \(B = \{11, 100, 00, 001\}\). Both these sequences look the same when written consecutively: \((001,100)=(00,11,00)=001100\). Whether a set is a code is a special instance of the post correspondence problem. I leave it to the reader to define the mapping.
If the carrier set is a code, we do not need to use the tuple syntax. For the following reasons a set might trivially be a code: All symbols have the same length. There are no overlaps (no non-empty prefix of one symbol is a suffix of another) between the symbols.
So for the first set \(S\) we do not need to use the tuple notation as it is always quite clear what is meant: \(S^2 = \{aa,ab,ba,bb\}\). Using this notation we now need a new symbol for the empty sequence and we usually use \(\varepsilon\) (epsilon). Note that concatenation follows these axioms: \(a\circ\varepsilon = \varepsilon\circ a = a\) (neutral element) and \((ab)c=a(bc)\) (associativity). The concatenation operation forms a monoid under the carrier set (a semigroup with identity).
Where does this confusion stem from? I think large part of it is that most programming languages do not properly support tuples in their type system in the way we want to use them in computer science theory. Programming langues do have tuple types but they are more rigid than what we want to use.
Let us look at python first:
# Python does have a native tuple type
>>> (3, 6)
(3, 6)
# We have an empty unit sequence
>>> ()
()
# Using the correct syntax we can nest this arbitrarily deep
>>> (((((),),),),)
(((((),),),),)
# We can construct one-tuples which are distinct from their value
>>> (3,) == 3
False
# The standard library has a sequence-product operation
>>> from itertools import product
# the cartesian product with itself works as we expect
>>> list(product([1,2,3], repeat=2))
[(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)]
# Having a zero-product returns the sequence that contains unit, which we expect
>>> list(product([1,2,3], repeat=0))
[()]
# Somewhat consistently, one-product returns the sequence of one-tuples but as seen above, this is not eqal to the original sequence
>>> list(product([1,2,3], repeat=1))
[(1,), (2,), (3,)]
# Also we do not have associativity
>>> list(product([1,2],product([3,4],[5,6])))
[(1, (3, 5)), (1, (3, 6)), (1, (4, 5)), (1, (4, 6)), (2, (3, 5)), (2, (3, 6)), (2, (4, 5)), (2, (4, 6))]
>>> list(product(product([1,2],[3,4]),[5,6]))
[((1, 3), 5), ((1, 3), 6), ((1, 4), 5), ((1, 4), 6), ((2, 3), 5), ((2, 3), 6), ((2, 4), 5), ((2, 4), 6)]
I also want to take a look at Haskell which is also interesting.
-- Haskell has native tuple types
> :t (3,5)
(3,5) :: (Num a, Num b) => (a, b)
-- But there is no singleton tuple type
> :t (5)
(5) :: Num p => p
> (5) == 5
True
-- We have the unit type that is inhabited with the single instance unit which we also can not nest
> :t ()
() :: ()
> :t ((((()))))
((((())))) :: ()
-- Checking for associativity is a type error as both nestings are distinct types and can not be compared via equals
Prelude> (1,(2,3)) == ((1,2),3)
<interactive>:6:2: error:
Prelude> :t (1,(2,3))
(1,(2,3)) :: (Num a1, Num a2, Num b) => (a1, (a2, b))
Prelude> :t ((1,2),3)
((1,2),3) :: (Num a, Num b1, Num b2) => ((a, b1), b2)
The type system does not allow us to even construct a type-safe product function as it is in python as the tuple size of the result sequence is dependent on the value of the argument (something like a -> Int:Val -> (a,)*Val). This would need dependent types. There is a generic function for the cartesian product with the type [a] -> [b] -> [(a, b)] which, as we have seen from the interactive session, would not obey the associativity law either.
We have seen that the tuple notation is just that: notation. It is not used for structure, only for disambiguity. If you want structure, you need to use uninterpreted functions \(t(1,t(2,3)) \neq t(t(1,2),3)\) that are not flattened. But programming languages and the type systems do see a structural difference in the tuple types. The 3-product in Haskell could have, depending on the implementation, three different types: [a] -> [b] -> [c] -> [(a,(b,c))] or [a] -> [b] -> [c] -> [((a,b),c)] or [a] -> [b] -> [c] -> [(a,b,c)] where we would expect all types to be the same.
Why did this article come to pass? Two reasons. During the database lectures we wanted to write up some database state (a set of rows for each table, a row being a sequence of column values) and while one table had three columns (\(\{(1,2,3),(4,5,6)\}\)) one table only had one column and for symmetry \(\{(1),(2),(3)\}\) was brought to paper which I remarked to be at least confusing for students as it might convey something not meant (there being a difference between the singleton tuple and the value).
The second example comes from computer science didactics, a module for the aspiring teachers. In a homework where some lesson had to be designed, one student had the topic of languages and grammars. In an example of a regular language they took this as an example alphabet: \(A=\{la,li,lu\}\). This is fine as the symbol of the alphabet are just syntax and are only of interest (as I've written above), in terms of whether the alphabet is a code or not and therefore which notation is used for concatenation operations. Now on a worksheet the following question was asked: \(lul \in A^*\). And this, I would claim, is a type error. The kleene closure of the alphabet only contains sequences of symbols from the alphabet (including the empty sequence) but "lul" is no sequence of symbols from the alphabet so it can not be of the same type (sequence from the alphabet) as the set (set of sequences from the alphabet). As the original alphabet was a code, all sequence can be written consecutively but it is unclear how "lul" can be deconstructed into elements of the alphabet. A possibiliy is, that the original alphabet was \(\{l,a,i,u\}\) and \(A\) was just a language over that alphabet but that was not written. For teachers, I believe, formalisms in that area are quite important.
This year I am teaching Java to first semester students. My own Java introduction has happened seven years ago. As I am quite interested in principles of programming languages I try to convey my enthusiasm for the topic and base my didactic methods around that. It's cool what we do. Let's talk about it.
I see the problems in a lecture for first semester students as they have yet to learn any theoretical basis for object oriented programming, that would be useful. In my oppinion one should start with the theoretical basis, like class hierarchies and the object model. But students only learn about partial orders (like a class hierarchy) later in the first year. So ideally (in my mind at least), a computer science education is without a computer for the first semester.
And because there is no theoretical basis, the approach taken by the professor is quite practical, and just barely supported by theory (wherever possible, but that's not much). This means that after the first lesson, students already know what a Hello World program looks like and they can fiddle with it. Even though they do not know what a class is, a static method, even methods or functions at all.
This leads to further problems down the road. We have an online platform where students have to solve programming assignments during seminars and as homework. But since they don't know about classes and class methods (or types or return statements for that matter), we can't have them implement classes, methods, or interfaces as homework and have to have them write output into the main method. That's a bad start, when you consider programming best practices.
Ideally one would like to start implementing small methods without function calls that implement some interface and then go on in creating more complex programs later on. But the problem is, that there is no way to run the java code without a main method. And even if you provide one, then the students can not really practice.
This shows how necessary a REPL or interactive interpreter is.
But Java has a few more problems that are quite bad for learners and can lead to confusion and misunderstanding.
For legacy reasons, Java has two kinds of types. There are primitive types that correspond in some manner to machine types, and the reference types that form the class hierarchy. Examples of primitive types would be int or float or void (Unit - only allowed as method return type). In general it's also the case that operators work on primite types but do not for reference types (exceptions apply). Those primitive types are builtin insofar that their type names are keywords as well.
As a homework for the second week I gave the following task: write a program that reads a number between 0 and 100 from the standard input (they don't know about standard input yet, and I'd prefer passing arguments as command line parameters but was overruled) and write a 10 character progress bar, visualizing the progress that correspond to the input number. This is my solution I worked from:
import java.util.Scanner;
class Progress {
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
int progress = input.nextInt() / 10;
int rest = 10 - progress;
while (progress > 0) {
System.out.print("|");
progress = progress - 1;
}
while (rest > 0) {
System.out.print("-");
rest = rest - 1;
}
}
}
Since this is quite complicated for beginners, I've given them the basic structure and removed all keywords, replacing them with % and replacing all variable names with #. Resulting in this:
import java.util.Scanner;
% Progress {
% % % main(String[] #) {
Scanner # = % Scanner(System.in);
% # = #.nextInt() / 10;
% # = 10 - #;
% (# > 0) {
System.out.print("|");
# = # - 1;
}
% (# > 0) {
System.out.print("-");
# = # - 1;
}
}
}
And as you can see, not entirely all type information is removed by replacing the keywords with #. If all types were reference types, we'd have a program that looked more like this:
% Progress {
% % Unit main(String[] #) {
Scanner # = % Scanner(System.in);
Integer # = #.nextInt() / 10;
Integer # = 10 - #;
% (# > 0) {
System.out.print("|");
# = # - 1;
}
% (# > 0) {
System.out.print("-");
# = # - 1;
}
}
}
Now doesn't this look quite a bit better? Some types are introduced as keywords but all user-created ones are not (and by user-created, I also mean the standard library). This is an inconsistency that is quite hard to explain away, even more so if you have yet to introduce the students to the vocabulary to explain this.
There are even more problems quite soon. Once conditionals are introduced, we have the next problem. The language construct if () then {} else {} only works with the bool type as conditionals. So primitive types are necessary to use the language constructs for conditional execution (while as well, but the numeric comparison follows somewhat naturally).
I do not know whether we will get this far, but for type parameters (for for polymorphic types, like containers) the primitive types don't work either.
All in all, I'd say Java would need to do away with primitive types and consistently use reference types. But for this to work properly with the operators, one would probably also need to add operator overloading. Once you're there, you could think long and hard about whether you'd really need the new keyword for instance construction.
And of course, one would want to introducing a proper Unit type. But since in Java all types are inhabited by the value null (who the hell had that idea?), this would be useless. So I will allow keeping the void keyword.
A friend recently had an interesting problem for me: There's a game for mobile phones where you have to exchange or transmute wares into each other, in order to create some strange supply chain.
Example of an earlier level.
A very complex later example.
The game is bleentoro, image copyright by them.
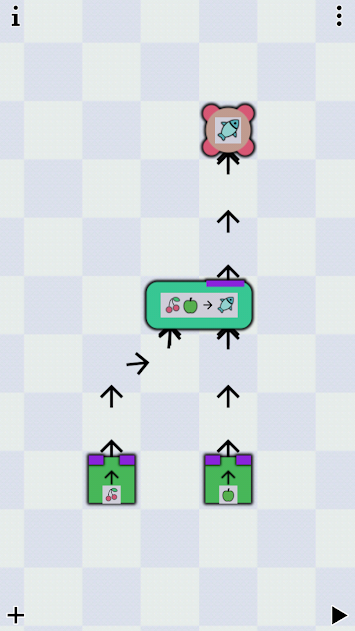
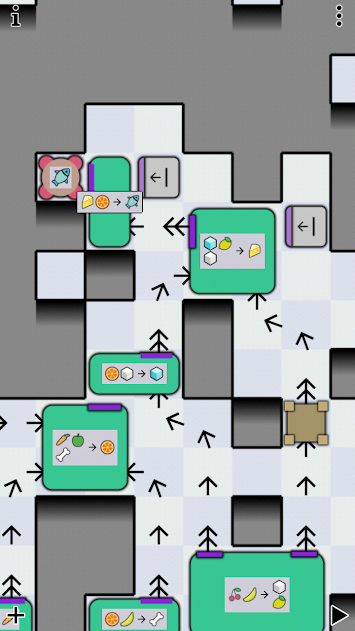
In this example (an earlier level) the goal is to create fish. We can transmute or exchange (I will only write about exchange from now on) an apple and a pair of cherries for a fish. Apple and cherry we have, or are created from thin air, in the context of the game. As you can see in the other example, this can get very complex.
The question is, given some input we have, in what order do we have to use the stations for exchange to create some output. How do we best model this problem?
From a previous article we already know that we can encode numbers in Prolog terms using Peano numbers. Using these we can match terms that represent at least or exactly some number. Exactly 3 would be s(s(s(z))) while at least 3 would be s(s(s(X))) with the variable X representing the rest of the term for some \(n\) so that \(3 + x = n\).
Let's start with a small example: we have an aunt that gives us apples. We have bob who is willing to exchange an apple for two berries. And we have a cousin who will bake a cake if we give them two apples and five berries.
Let's formalize our rules in some way:
a: / -> 1A
b: A -> 2B
c: 2A, 5B -> 1C
We model this as some kind of inventory(A, B, C) with some slots for Peano encoded numbers. Meaning that inventory(s(z), z, s(C)) means an inventory of exactly one apple, zero berries, and at least one cake. Lucky us.
Let's define our possible exchanges as Prolog facts with exchange(Kind, Pre, Post) meaning we use the exchange method Kind and we get from inventory state Pre to inventory state Post. If we lose an item, we have it in Pre but don't in Post. If we gain one, it's the other way around. Of course, the rest of our inventory should stay the same.
exchange(a, inventory(A, B, C), inventory(s(A), B, C)).
exchange(b, inventory(s(A),B,C), inventory(A, s(s(B)), C)).
exchange(c, inventory(s(s(A)), s(s(s(s(s(B))))), C), inventory(A, B, s(C))).
As we can see, we can encode basically any numeric condition that uses only "just exactly" and "at least", as well as addition and subtraction and "setting" fields to specific values. If we have to give at least three apples, but all of them, to get a cake, the rule would be exchange(c, inventory(s(s(s(_))), B, C), inventory(z, B, s(C)))..
We want to create a predicate trades(Start, Goal, Path) where we give a Start inventory and a Goal inventory and want to get a Path of exchanges. The most obvious approach is the following:
trades(Goal, Goal, []).
trades(Start, Goal, [H|T]) :- exchange(H, Start, Temp), trades(Temp, Goal, T).
So we're done when our Goal is reached. And if not, we have to try some exchange. We try it and we quickly learn that...
?- trades(inventory(z, z, z), inventory(_, _, s(z)), Path).
ERROR: Out of local stack
... it doesn't work.
The problem is, that calling the exchange predicate in the recursive call always tries the first rule first and since that basically always works, we get into an infinite loop. Let's reorder the rules and put the generating rule first.
?- trades(inventory(z, z, z), inventory(_, _, s(z)), Path).
ERROR: Out of local stack
It still doesn't work. Let's look at the trace.
[trace] ?- trades(inventory(z, z, z), inventory(_, _, s(z)), Path).
Call: (8) trades(inventory(z, z, z), inventory(_700, _702, s(z)), _712) ? creep
Call: (9) exchange(_960, inventory(z, z, z), _984) ? creep
Exit: (9) exchange(a, inventory(z, z, z), inventory(s(z), z, z)) ? creep
Call: (9) trades(inventory(s(z), z, z), inventory(_700, _702, s(z)), _962) ? creep
Call: (10) exchange(_978, inventory(s(z), z, z), _1002) ? creep
Exit: (10) exchange(b, inventory(s(z), z, z), inventory(z, s(s(z)), z)) ? creep
Call: (10) trades(inventory(z, s(s(z)), z), inventory(_700, _702, s(z)), _980) ? creep
Call: (11) exchange(_1000, inventory(z, s(s(z)), z), _1024) ? creep
Exit: (11) exchange(a, inventory(z, s(s(z)), z), inventory(s(z), s(s(z)), z)) ? creep
Call: (11) trades(inventory(s(z), s(s(z)), z), inventory(_700, _702, s(z)), _1002) ? creep
Call: (12) exchange(_1018, inventory(s(z), s(s(z)), z), _1042) ? creep
Exit: (12) exchange(b, inventory(s(z), s(s(z)), z), inventory(z, s(s(s(s(z)))), z)) ? creep
Call: (12) trades(inventory(z, s(s(s(s(z)))), z), inventory(_700, _702, s(z)), _1020) ? creep
Call: (13) exchange(_1040, inventory(z, s(s(s(s(z)))), z), _1064) ? creep
Exit: (13) exchange(a, inventory(z, s(s(s(s(z)))), z), inventory(s(z), s(s(s(s(z)))), z)) ? creep
Call: (13) trades(inventory(s(z), s(s(s(s(z)))), z), inventory(_700, _702, s(z)), _1042) ? creep
Call: (14) exchange(_1058, inventory(s(z), s(s(s(s(z)))), z), _1082) ? creep
Exit: (14) exchange(b, inventory(s(z), s(s(s(s(z)))), z), inventory(z, s(s(s(s(s(s(z)))))), z)) ? creep
Call: (14) trades(inventory(z, s(s(s(s(s(s(z)))))), z), inventory(_700, _702, s(z)), _1060) ? creep
Call: (15) exchange(_1080, inventory(z, s(s(s(s(s(s(z)))))), z), _1104) ? creep
Exit: (15) exchange(a, inventory(z, s(s(s(s(s(s(z)))))), z), inventory(s(z), s(s(s(s(s(s(z)))))), z)) ? creep
Call: (15) trades(inventory(s(z), s(s(s(s(s(s(z)))))), z), inventory(_700, _702, s(z)), _1082) ? creep
Call: (16) exchange(_1098, inventory(s(z), s(s(s(s(s(s(z)))))), z), _1122) ? creep
We're still running into an infinite loop since we're just getting apples and trading them for berries.
There's a trick if our solution is a list. If the length(List, Length) predicate is called with both predicates free (length(L, _) for example), we get lists of increasing length as solutions. So if we can bind our solution to lists of increasing length, we won't get infinite loops of apple-berry-exchanges without ever trying short solutions.
So our query now looks like this:
?- length(Path,_), trades(inventory(z, z, z), inventory(_, _, s(z)), Path).
Path = [a, b, a, b, a, b, a, a, c] ;
Path = [a, b, a, b, a, a, b, a, c] ;
Path = [a, b, a, b, a, a, a, b, c] ;
Path = [a, b, a, a, b, b, a, a, c] ;
Path = [a, b, a, a, b, a, b, a, c] ;
Path = [a, b, a, a, b, a, a, b, c] ;
Path = [a, b, a, a, a, b, b, a, c] ;
Path = [a, b, a, a, a, b, a, b, c] ;
Path = [a, b, a, a, a, a, b, b, c] ...
As it turns out, there are a few ways to do it, but nothing shorter than 9 trades. We can even look, whether we have anything left over after we got our cake:
?- length(Path,_), trades(inventory(z, z, z), inventory(A, B, s(z)), Path).
Path = [a, b, a, b, a, b, a, a, c],
A = z,
B = s(z) .
Yeah. As it turns out, we have a berry to spare.
This is how you do it. And of course, you could simulate a shop with that, as one inventory slot could be the number of coins. If the inventory gets too large, you can split it into item types so you don't have to copy every unchanged item from the pre-condition to the post-condition. Then you can copy a term that might represent any number of items.
But beware: this algorithm (with Prolog's evaluation scheme) has not so good complexity. For a solution of length \(n\) and \(m\) rules it has a run time of \(O(m^n)\). We create every possible solution list permutation but break early, if no rules are applicable.
Depending on our instantiation of Start and Goal, this algorithm doesn't terminate (if the system isn't terminating, the algorithm isn't either). Our system doesn't terminate as we can always apply a again and again. We're creating increasingly longer partial solutions which might turn out to be no solution at all. If there is no solution, you won't know. The algorithm just tries longer and longer lists trying to find a solution.
If you have any other conditions on your solution (some exchanges might be limited or necessary) you can put most of them after the trades call. Some conditions, like membership, can be put before.
Let's say we have a terminating system by taking away the a rule. If our Start is fully instantiated, then our algorithm terminates. Let's try another query and find out, with how many apples we need to start to get a cake:
?- trades(inventory(A, z, z), inventory(_, _, s(z)), Path).
ERROR: Out of local stack
Through the unification rules, it is possible that a rule creates terms on the left side of the rule. In this case, the algorithm tries to give us increasing amounts of berries to match that with the starting condition (only rule b is applied in reverse, always leaving us with one cake, which doesn't match the starting condition). There we need the length predicate.
?- length(Path,_), trades(inventory(A, z, z), inventory(_, _, s(z)), Path).
Path = [b, b, b, c],
A = s(s(s(s(s(_2334))))) .
We need at least five apples for a cake. But we knew that.
To recap:
I think, there's a different approach using linear programming. I might try that in the future.
I love watching 8 Out Of 10 Cats Does Countdown. It's a british panel show where a few comedians solve word puzzles and mathematics puzzles. It's based on the game show Countdown that's been running since 1982.
And I also like the host Jimmy Carr very much.
The show consists of three different puzzles:
In the Letters round a team (or single contestant) picks 9 consonants and vowels from their respective piles. After the team chooses from one of both piles, the letter is revealed and put up on the board. They then choose again until 9 letters are on the board. After all letters are on the board, the teams have 30 seconds to form a word out of as many of the letters as possible. The team with the longest word scores that many points.
Letters Round
In the Conundrum a list of letters that already spell out a funny group of words is given by the host and the contestants try to find a 9 letter anagram. The first team to buzzer in the correct answer gains 10 points. This is the final round of the game.
Conundrum
In the Numbers round a team (or single contestant) picks 6 numbers from two piles. A random number is picked and the contestants have to create a mathematical formula out of the picked numbers that equal the target number. The specific rules follow.
Numbers Round
According to Wikipedia there are 6 columns of 4 numbers (4 rows). One column contains the numbers 25, 50, 75, and 100 and the other 5 columns contain the numbers 1 to 10 twice each. That's not exactly the same as on the show, as there appear to be 7 columns of 4 numbers but not every stack has all 4 number cards.
Contestants choose a total of 6 numbers from the "small" and "large" columns. The usual pick would be 2 to 3 "large" numbers and the rest small ones.
Then a random number between 100 und 999 is generated. The contestants try to create a mathematical formula that has the random number as the result. In the formulare only the following operations are allowed:
The contestants do not have to use all the numbers to get the target number.
Finished Numbers Round
Since I am really not good at this, I wrote a solver for the numbers game in Haskell.
How do we go about this problem? First of all, we have to decide on a data structure. Let's start with a traditional term structure where a Term is a binary operation and two terms, or an integer value. An Operation is the function mapping two integers to a third, and a string to pretty-print the operation. The mapping is not total and might fail.
data Term = Op Operation Term Term | Val Integer
data Operation = Operation {fun :: (Integer -> Integer -> Maybe Integer), name :: String}
instance Show Term where
show (Val x) = show x
show (Op op l r) = "(" ++ (show l) ++ (name op) ++ show r ++ ")"
Now we have to define our operations and what they should do. Since we're using Maybe, and it's a monad, we can use monadic notation where it suits us:
operations = [ Operation (\x y -> return (x + y)) "+"
, Operation (\x y -> return (x * y)) "*"
, Operation (\x y -> guard (x > y) >> return (x - y)) "-"
, Operation (\x y -> guard (x `mod` y == 0) >> return (x `div` y)) "/"
]
eval :: Term -> Maybe Integer
eval (Val v) = Just v
eval (Op o l r) = do l' <- eval l
r' <- eval r
(fun o) l' r'
As we can see, the preconditions to the subtraction and division are encoded using the guard function. If the function returns true, the whole operation returns Nothing, otherwise it returns Just the value.
Since Haskell uses lazy evaluation, we can define a list of all possible terms given a list of integers and filter for the ones that evaluate to the correct number.
As we create a Term we have to be careful to not use any of the numbers again. So we will split our numbers in two sets. One that can be used in the left Term of an Operation and the rest can be used in the right Term. We will create all terms using our definition. A Term is either the Value of one of the numbers for that subterm, or an operation with some numbers reserved for the left term and some numbers reserved for the right term.
terms :: [Integer] -> [Term]
terms nums = do n <- nums -- choose a number
[Val n] -- one solution
++
do op <- operations -- choose an operation
(l, r) <- subset_split nums -- choose a split
guard $ l /= []
guard $ r /= []
ls <- (terms l) -- choose a term for the left side
guard (eval ls /= Nothing)
rs <- (terms r) -- choose a term for the right side
guard (eval rs /= Nothing)
[Op op ls rs] -- one solution
For performance reasons we already evaluate the generated subterms in order to check whether the operations are valid. There are a lot of terms that can not be evaluated and we want to throw them out as early as possible (or not even generate them).
We haven't defined subset_split yet. The idea is, to just split the list of numbers in two groups in every possible way:
subsets :: [Integer] -> [[Integer]]
subsets [] = [[]]
subsets (x:xs) = subsets xs ++ map (x:) (subsets xs)
subset_split nums = do l <- subsets nums
return (l, nums \\ l)
Now all that remains is to generate all terms given a set of numbers, evaluate them, filter out the ones that don't have the correct value, and return the first one:
solve :: [Integer] -> Integer -> Maybe Term
solve nums target = let possible_solutions = map (\x -> (x, eval x)) (terms nums)
solutions = filter (\x -> (snd x) == (Just target)) possible_solutions
in listToMaybe $ map fst solutions
And in our main we only read the list of numbers and the target as arguments and print the solution:
main = do args <- getArgs
let nums = (read (args !! 0))::[Integer]
target = (read (args !! 1))::Integer
print $ solve nums target
And there we go:
$ ./countdown "[100, 75, 2, 10, 3, 8]" 746
Just (8+(3+((75*(100-2))/10)))
Our solution is \(8+3+{{75*(100-2)} \over 10}\) while the solution from the show was \(10*75 - {8 \over 2}\).
As you can see, we do not always get the easiest solution but we usually have a solution quite fast. This one took about a tenth of a second. The 30 seconds given to the contestant are usually quite enough. To make sure we had the "nicest" solution, we probably would need to generate all terms and sort them by size. The smallest one should be the nicest one.
Theme based on notmyidea